Triangles to Order
Seventh Grade Poster Problem:Geometry
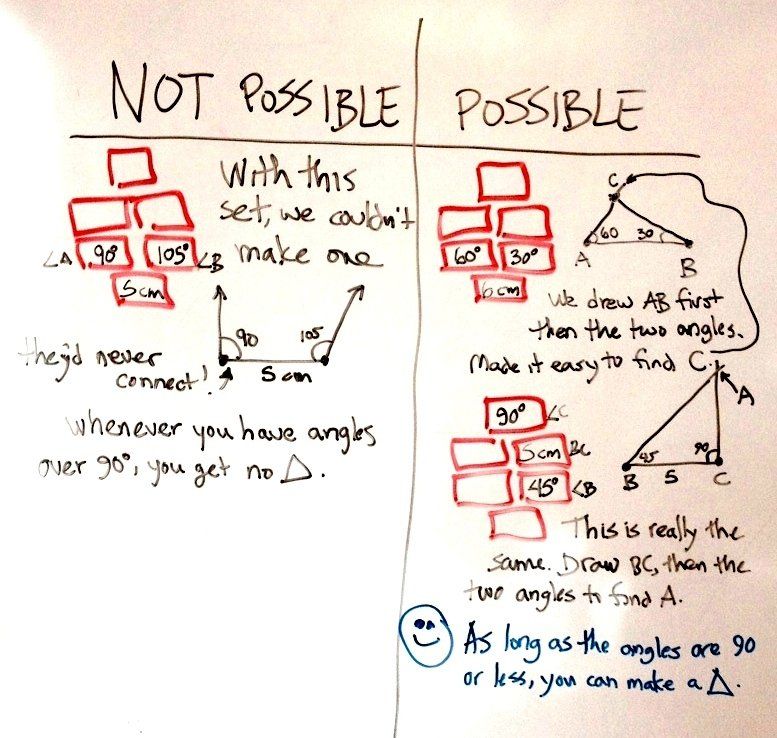
In this poster problem, students try to build triangles to particular specifications (specs). The specs can include side lengths, angles, or a combination of both.
Downloadable Materials
Students go on to generalize, and develop an understanding about when they can determine a triangle from partial information and when they cannot.
Learning Objectives:
- Students construct triangles according to specifications (angle and/or side measures).
- Students recognize that with three conditions, you can often—but not always—determine a triangle.
- Students begin to understand the rules for when three conditions determine a triangle.
Common Core State Standards for Mathematics:
- 7.G.A.2
Materials:
Scissors, Rulers, Protractors, Scratch paper. Lots of scratch paper.
Teacher Tune Up:
Using protractors. Many students have little experience using protractors—or with angle measure at all, for that matter. Ultimately, we want students to be able to use a protractor to construct or measure angles up to 180° to the nearest degree.
The issue of whether two triangles are the same (i.e., congruent). We do not make a big deal about that here, but if it comes up, there are two main ways to look at it, described in Triangles and Constraints. The main point is that two triangles are the same if they have the same size and shape. Another way to say it is that they’re the same if you can cut one triangle out (or make a transparency of it) and move it, turn it, and flip it to match the other exactly.
1. LAUNCH
This lesson will be all about triangles. Explain why triangles are important, for example, “triangles are at the center of geometry. If you understand triangles—really understand them—you’ll be in great shape. One reason is that you can make things out of triangles. In fact, most realistic computer graphics, from games to movies, are made up of triangles.”
Show Slide #1:
These are “wireframe” drawings. An animator would color the triangles and use more of them to make smoother, more realistic heads.
Ask, “What do you need to know to determine a triangle? After all, rectangles are easy: if you know the height and the width, you have the rectangle. But what do you need to know for a triangle?”
Show Slide #2:
Ask: what are all the numbers on this diagram? What do they mean?
- 5 cm is the length of AB and AC.
- 7.1 cm is the approximate length of BC.
- 45° is the measure of ∠B or ∠C.
- 90° is the measure of ∠A.
Suppose you’re on the phone with somebody and they’re trying to describe this triangle.
What do they have to tell you before you can draw the triangle?
- Here’s the point, which you can elicit in discussion: they don’t need to tell you all of the information in the picture. Suppose they left out the 7.1 cm for the long side. You could still draw the triangle using the rest of the information. How little information do you need?
Possible mini-activity:
If students need additional reinforcement…
- Have students work in pairs. The “teller” faces the screen or board, and the “drawer” faces away.
- Teacher draws or displays a different triangle (for example, the one on Slide #3)
- The teller tries to get the drawer to draw the triangle using as few clues as possible. (A “clue” is one of the numbers on the slide.)
2. POSE A PROBLEM
Make sure students have rulers, protractors, scissors, scratch paper.
Each group gets Handout #1
and several copies of the recording sheet, Handout #2. (If a group runs out of Handout #2, they can use scratch paper if they record carefully.)
Have students cut out the cards at the bottom of Handout #1 (leaving the “form” in the top half of the handout intact). Mix them up and put them face down.
Explain the setting: Imagine your friend is trying to tell you how to draw a particular triangle. He/she give you three pieces of information as a “specification.”
Tell students to draw three cards and place them on the form. Explain that this represents your friend telling you the three parts of the specification.
- Lengths go in the three rectangles labeled AB, AC, or BC. Those are side lengths.
- Angles (with °) go where you see ∠A, ∠B, or ∠C.
The group must agree about whether the specifications tell you what you need to make the triangle.
- The group must agree whether the specifications will let you make just one triangle, two triangles, no triangles at all, or “many” triangles—an infinite number.
- If you can make just one triangle, you should draw it carefully using the ruler and protractor.
- If you can make two triangles, you should draw them both.
- If you can make zero or a large number of triangles, you should be ready to explain how you know.
- When that’s done, set the little cards aside and start a new triangle using the face-down cards.
Try to solve as many different configurations as you can.
When to end the student activity
This is a judgment call: ideally every group has encountered a situation in which they made a single triangle, and another situation in which the triangle was impossible.
3. WORKSHOP
Arrange students in groups. They should still have their form and the cards from Phase 2 of the lesson (Pose a Problem). They should also have records of specifications they used.
First hold a brief discussion about what happened during Phase 2. You might ask:
- Did you find specifications that gave you just one triangle?
- Did it matter which points they referred to? (In general, yes)
- What order did you draw this triangle in? That is, which clue did you use first? Which was second?
As students report, be alert for misunderstandings:
- Be sure that students always fill three cells out of the six available on the form.
- Be sure sides and angles go in the right slots.
- Be sure students are paying attention to which vertices are which.
Distribute Handout #3. Explain that each group will divide their poster into two columns and follow the instructions on the handout.
Help for “two” and “many”
Some groups may have trouble finding examples of specs that yield two or more triangles. Here are ideas about how to help.
- Suggest that they try specifications with three angles. And if the triangle is impossible, they should ask themselves what would have to be different in the spec to make the triangle work.
- Look to see if they have an SSA situation—one with two sides and the angle that is not between the two sides, e.g., AB, AC, and ∠B. Have them play with that, experimenting with different values. If they still have trouble, suggest they use a very small angle, such as 15°.
4. POST, SHARE, COMMENT
Have students post their posters around the classroom.
Encourage students to travel around the classroom to view the posters created by other groups. Students should be encouraged to pose questions to other groups by attaching a small adhesive notes to their posters.
During this time, the teacher should review all the posters and consider which to highlight during the subsequent discussion.
Sample Posters
5. STRATEGIC TEACHER-LED DISCUSSION
Select a sequence of posters to use during the teacher-led discussion that will help move all students from their current thinking (often Levels 1–3 below) up to 4 or 5.
Level 1:
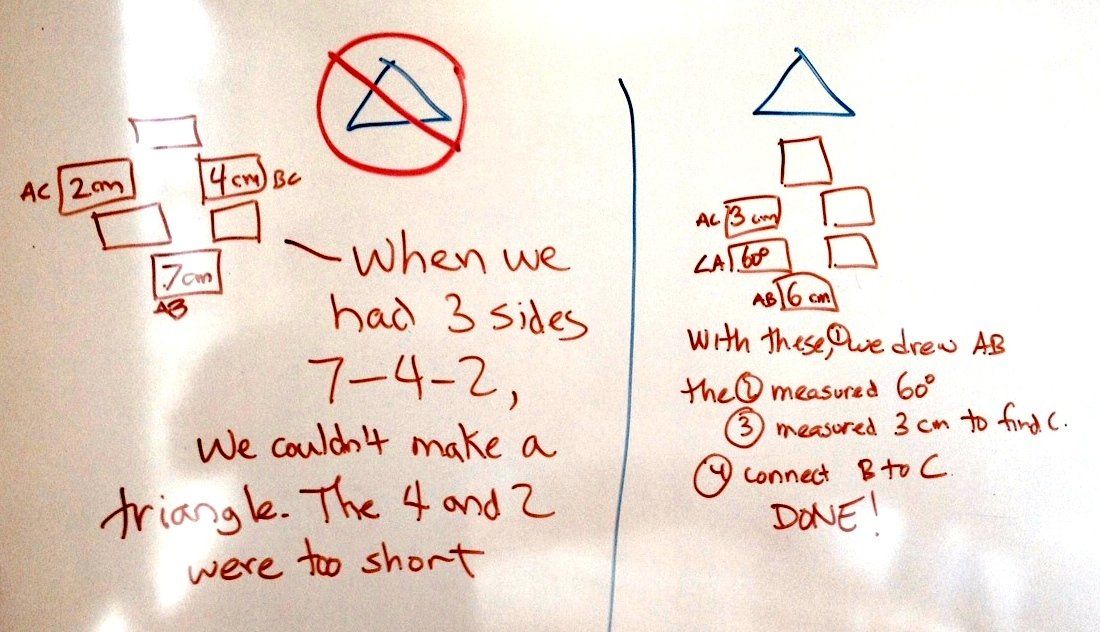
Students found examples of specs that make no triangles and one triangle. But the explanations (the why and how) are specific to the numbers and do not address the reasons. (“Our sides were 5, 3, and 1. With those lengths, we couldn’t make a triangle.”)
Level 2:
Like Level 1, but the group uses the numbers to create correct reasons. (“Our sides were 5, 3, and 1. Since 3 + 1 = only 4, the two short sides are not long enough to make a triangle with 5 on the other side.”)
Level 3:
Students move beyond the specific numbers in their explanations (“Our sides were 5, 3, and 1, but to make a triangle the long side has to be less than the sum of the other two”) but do not group triangles together with others in the same category (e.g., one with sides 7-4-2).
Level 4:
Students create coherent reasons and descriptions that go beyond the specific numbers and recognize that other triangles are in the same categories. (“Any time you have side AB with angle A and angle B [and A + B is less than 180°], just draw side AB first, then make the two angles. Where the angle-lines meet is point C. Connect them up to make your triangle.”) Students may explain situations with two or more triangles.
Level 5:
Students recognize that it’s not the specific points and labels that matter, but rather the relationship between them. (“Any time you have a side and the two angles on either end of it, draw the side first—that give you two points—and then the angles. The angle-lines meet at the third point…”) Students can explain the cases where you get two and many triangles coherently.
Supporting Generalization
Help early presenters generalize. For impossible triangles, ask, “!s there a way I could change one of these numbers and have the specs make a triangle?” From there, help the class figure out the criteria for impossibility.
For a unique triangle, ask the class, “Are these specifications the same sort as the others we’ve seen, or are they different? Could they use the same procedure to draw the triangle as these other triangles?” That way, the class can see that making a triangle by specifying 3 sides is different from 2 sides and the included angle, etc.
Connecting across groups
As students present, keep a list of the types of impossible specifications and the ways you can make a unique triangle. You will need to update them as students generalize better; avoid imposing your own wisdom.
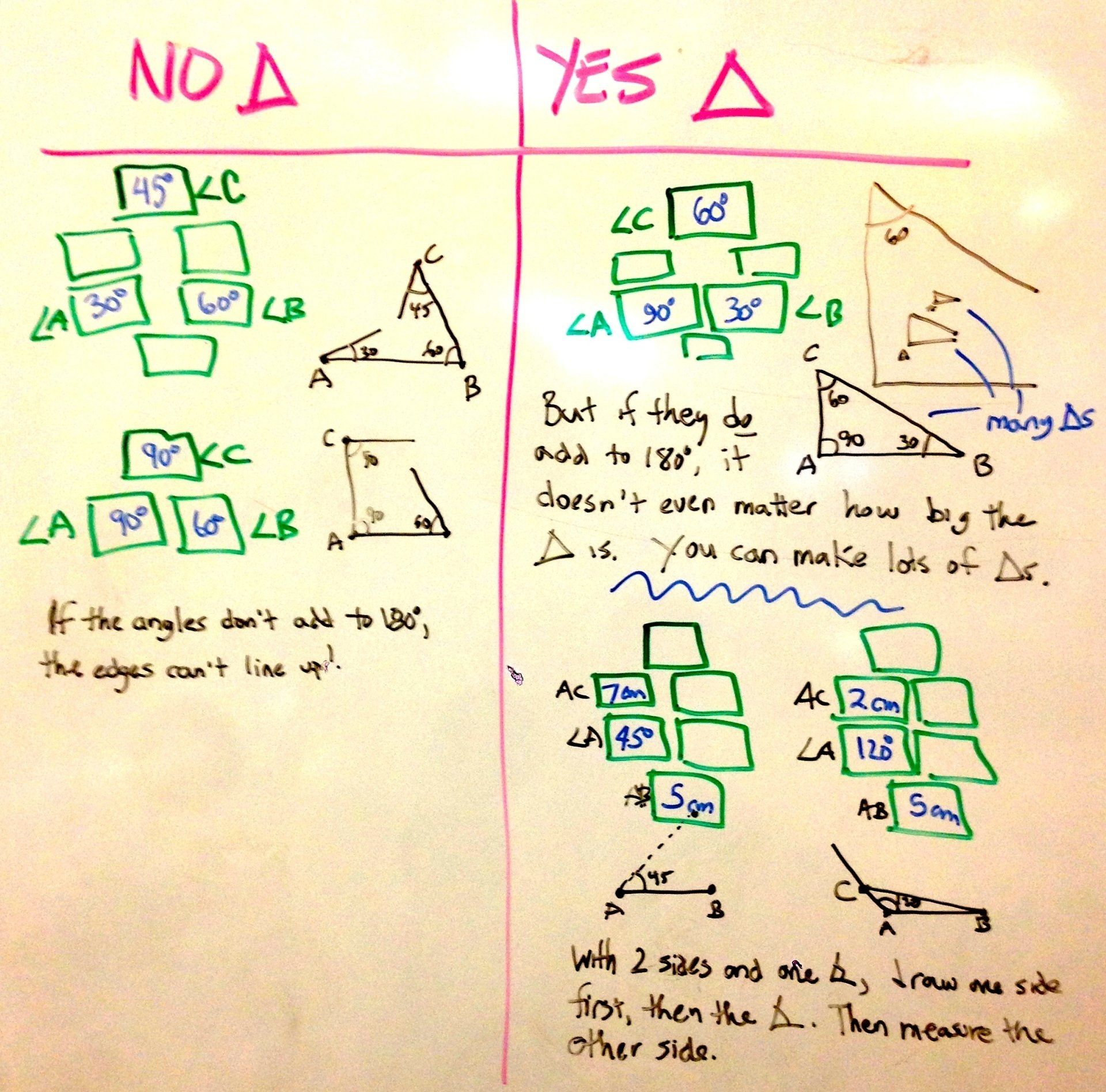
How can three clues fail to make a triangle?
- Triangle inequality: with three sides, the longest is longer that the sum of the other two.
- Angles too large: the sum of two angles exceeds 180°.
- Swing-and-a-miss: suppose you have AB = 3 cm, BC = 4 cm, and angle C is 90°. If you make BC first, then angle C, it’s clear that AB can’t “reach” to the other side.
- And how can three clues make a triangle (provided that they don’t meet one of the impossibility criteria above)?
- Three sides (SSS). This can be difficult without a compass; use guess and check to get close.
- Two sides and the angle between (SAS). Always works. Order doesn’t matter.
- Two sides and a different angle. Depends on the details; you could get zero, one, or two. Start with the side connected to the angle.
- Two angles and the included side (ASA). Works if the angles aren’t too big. Draw the side first.
- Two angles and a different side (AAS). Hard unless you know about 180°; guess and check.
Three angles: the miracle of 180°
Students may not know the 180° rule; this is a good time to expose them to it—especially if they discover it themselves. One consequence: If your clues are three angles that add to 180°, you get an infinite number of triangles. All the triangles will be the same shape, but of any size. They’re “similar” instead of “congruent.”
Some students may object to calling the similar triangles different. There are at least two responses: one is to explain that it’s a convention. Another, perhaps more to the point, is that if you were building something (a table top, say) and you made it a different size, it wouldn’t matter that it was the right shape—it would not fit.
How you get two possibilities
One way is on Handout #4, problem #5.
6. FOCUS PROBLEM: Same Concept in a New Context
Pass out the Handout #4
for this problem (“Focus Problem: Zero, One, Two, Many”)
Handout #4 Answer Key
Answers
- One triangle (ASA).
- One triangle (SAS).
- One triangle (Hypotenuse-leg; angle C is 90°).
- One triangle (Two angles give a third—60°—and you have ASA. This result is similar to #3).
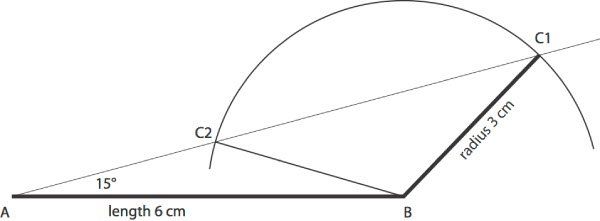
- Two triangles, at last! This is SSA. See the illustration below. If you make side AB (6 cm) and angle A (15°), you now have to figure out side BC (3 cm). Imagine it swinging from point B. It can rest its end on the line coming out of A in two places, marked C1 and C2. Either of these could be the third vertex of the triangle.
- No triangles. Sum of angles is too great.
- Many triangles, all similar (Sum of angles is 180°).
- No triangles, because of the triangle inequality: the two 2-cm sides are not long enough to meet opposite the 5-cm side.
More about Answer #5:
Project funding provided by The William and Flora Hewlett Foundation and S.D. Bechtel Jr. Foundation.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.