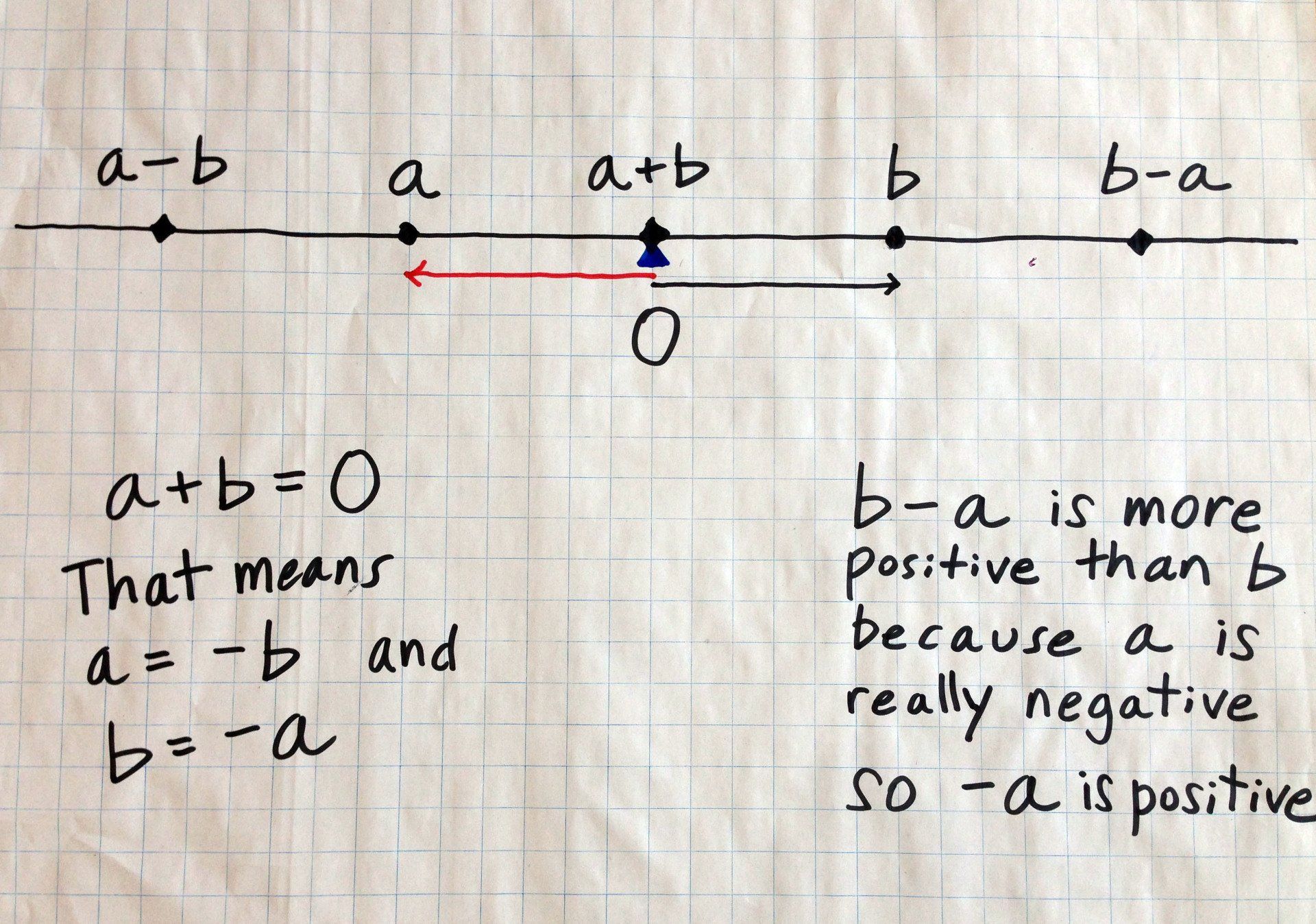Seeing Sums
Seventh Grade Poster Problem:The Number System
Unlike other poster problems, this problem is about mastering a mathematical model, the number line model for sums, rather than using the model to solve a “real life” problem. The model will spark a discussion in which your students will use language and reasoning highlighted in the CCSSM. In the launch, you will first set the stage by asking students to consider limitations of the familiar set model for sums and differences. Then, you can introduce the number line model using a short animation. Next, the students explore the model, first by hand, and then with a dynamic number line game. Finally, in the concluding discussion, you will use the model to elicit key ideas from your students.
Downloadable Materials
Learning Objectives:
- Represent addition and subtraction on a number line diagram.
- Understand p + q as the number located a distance |q| from p. The direction depends on whether q is positive or negative.
- Understand subtraction as adding the additive inverse. p − q = p + (-q)
- Use the number line model to show that the sum of two opposites is zero.
- Use terminology such as additive identity, opposite, additive inverse, and absolute value to reason about relationships among rational numbers.
Common Core State Standards for Mathematics:
- 7.NS.A.1a–1d
1. LAUNCH
Start by accessing prior knowledge:
Do you remember learning to add and subtract in elementary school? For example, the problem 6 − 4 might be shown with a story: ‘I have 6 apples and I give 4 away. How many do I have left?’ Here is a familiar picture of that story.
Show Slide #1.
But, this story and picture don’t work so well when you want to take away more than you have. For example, what happens when you try to do 6 − 8?
Show Slide #2.
Ask, “What is wrong here?”
You could then say:
What does it mean to take away something you don’t even have? Well, mathematically, we use negative numbers to reason about these situations. But this is where a new model can help understand what is going on. When we do addition and subtraction with negative numbers it can be helpful to use a new story--or model--one that is more flexible than the 'set model' above. The number line model offers a consistent model for addition and subtraction that works for integers and all rational numbers. It will be useful in both middle school and also in high school mathematics.
2. POSE A PROBLEM
Say to students: Now that you have seen a short demonstration, now is your chance to practice using the number line to represent sums.
Handout #1
(2 pages) asks you to create a number line diagram for 5 sums with numbers, and 7 sums with letters.
Handout #1 Answer Key
3. WORKSHOP
Open the dynamic number line model
and demonstrate how the model shows the sums and differences.
Directions to the students: "In this workshop you will work with a classmate to develop a deeper understanding of the number line model for sums."
Part 1:
Allow students 10–15 minutes to experiment with the dynamic representation for number line sums. They should play the game with a partner, or in a group (fewer than four students is ideal so all students can have a chance to be player 1 and player 2).
Students might start by guessing. Push them to generalize by asking them to talk about strategies for identifying (a + b), (b – a), and (a – b) the first time. If the model with no numbers is confusing at first, they can click the button to show the numbers on each number line.
Part 2:
Each pair or group of students should now create a poster that shows a guide for locating sums when no numbers are visible.
You could tell students, “For your poster, draw a number line with zero marked (but no other numbers) and pick positions for a and b. Find positions for (a + b), (a – b), and (b – a). The poster should show interesting or challenging configurations.”
Encourage each group to write three generalizations that they noticed as they work with the number line. For example, they might write “when a and b are equal, we know that a – b is at 0 because anything minus itself is zero.”
5. STRATEGIC TEACHER-LED DISCUSSION
In this discussion, you will use the students’ posters to solidify understandings of adding negative and positive numbers. Ask the students to explain their strategies. At first the students will struggle to explain how they know the right answer, and they will probably use imprecise language. During this time, teacher and students can start using more formal vocabulary to help clarify explanations. In this discussion, your students will to use key terminology like opposite, absolute value, and additive inverse. Using the terms in this meaningful and relevant context is intended to deepen their understanding.
Using the sample posters in the previous section, the following guide is ordered roughly by level of complexity, beginning with the most intuitive example of a and b as both positive is first. Beyond these five samples, students can consider other interesting configurations in which a = b.
Discussable math from Poster A (a and b are both positive and a > b)
This case is familiar to students, but they may not have formalized their understandings. Here are three generalizations:
- (a + b) is to the right of both a and b because both a and b are positive.
- (a – b) is positive and less than a because b is positive and less than a (think of 5 – 3 = 2 as an example).
- (b – a) is negative because we are subtracting a larger positive number from b (for example 3 – 5 = -2).
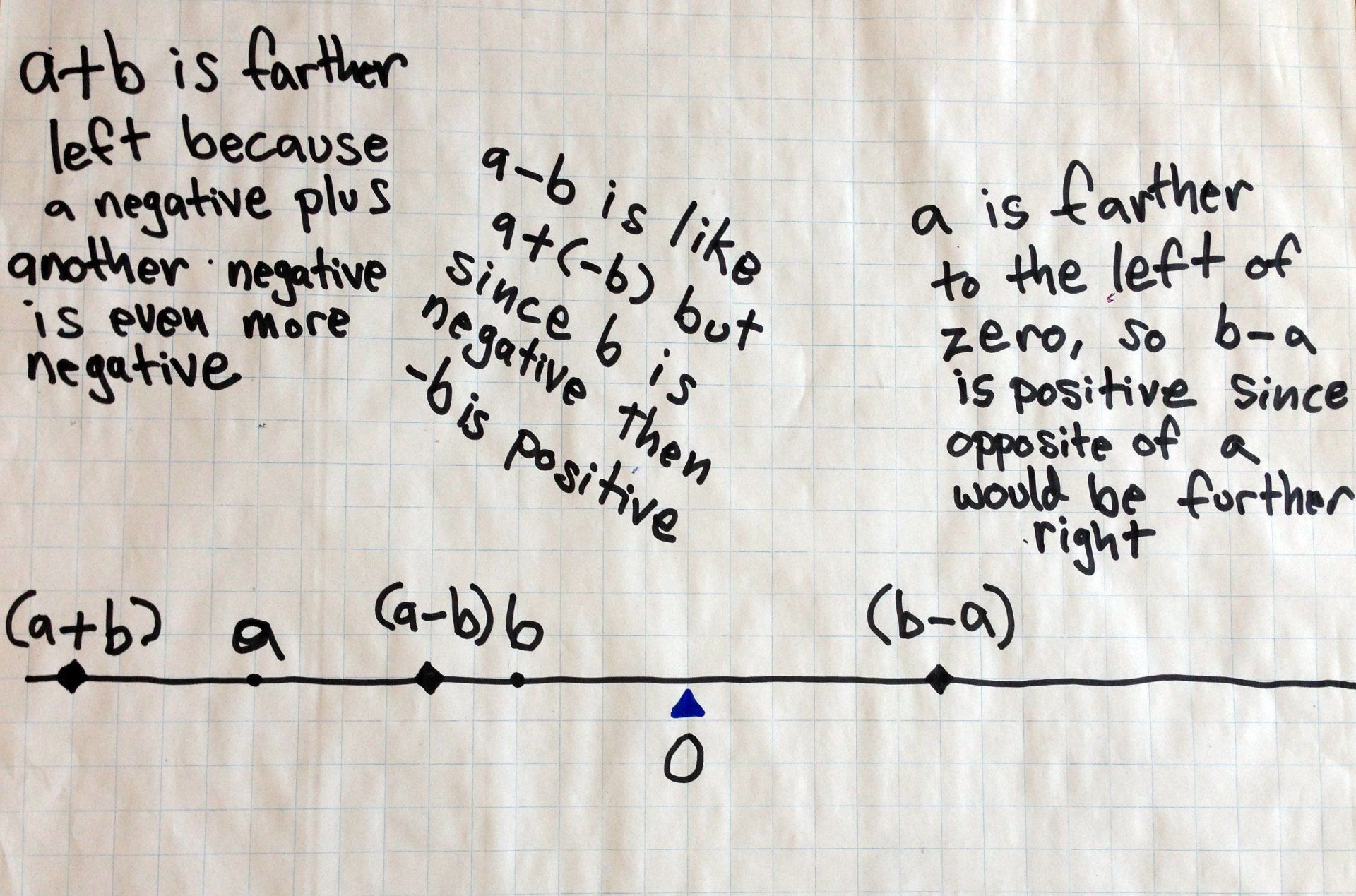
Discussable math from Poster B (a and b are both negative with a < b)
- This might be the most challenging poster for students to explain.
- In this poster, we can see that a + b is the farthest to the left because a negative number plus another negative number is negative. Students might say a + b is “a larger negative number.” This can be re-stated as (a + b) has a larger absolute value.
- (a – b) is located between a and 0. Students might notice that they can re-write subtraction as addition: (a – b) = a + (-b). Since b is negative, the opposite of b, that is, -b, is positive so a + (-b) is to the right of a.
- (b – a) is to the right of 0--it is positive. One way to explain this is that b – a = b + (-a). But remember, since a is negative, -a is positive. Also, since a is farther from zero (formally written in terms of absolute values, |a| > |b|) this tells us (b – a) will be positive.
Discussable math from Poster C (a and b are opposite signs and equally distant from zero)
- Students might like the symmetry in this poster.
- In this case, we see that a + b = 0. This tells is that a = -b and b = -a. In other words, a and b are opposites. This is a special situation--adding two numbers and getting zero means the numbers are additive inverses of each other. (You could highlight how the additive inverse plays a major role in solving algebraic equations like x + 4 = 12).
- We also see that (a – b) is less than a. This makes sense because b is positive and a – b = a + (-b).
- Finally, (b – a) is positive and greater than (to the right of) b because (b – a) = b + (-a) and, don’t forget, -a is positive.
Discussable math from Poster D (a and b are opposites but are not equally distant from zero; a > b)
- Here we can see that (a + b) is between a and b. This is because a and b have opposite signs. However, we can tell that a ≠ -b because a + b ≠ 0 (as in Poster C).
- (b – a) is less than b because (b – a) = b + (-a) and adding the opposite of a to b has the same effect as adding two negative numbers.
- Finally, (a – b) is greater than a because b < 0 and a – b = a + (-b). Since b < 0, -b > 0 and a + (-b) is the same as adding two positive numbers.
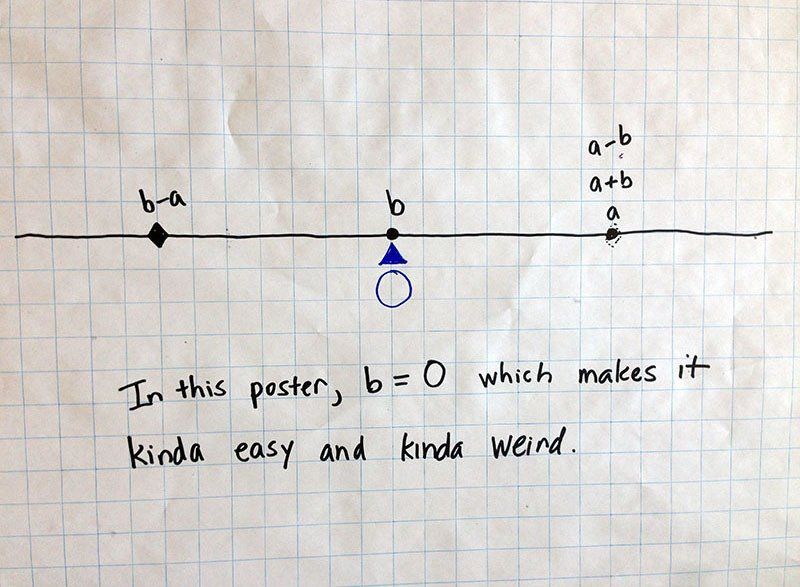
Discussable math from Poster E (One of the numbers is 0)
- Note that in this picture, a, (a + b) and (a – b) are all at the same point on the number line.
- In this poster, b = 0. When b is zero, a + b = a + 0 = a. 0 is called the additive identity and it plays an important role throughout math.
- (a – b) is also equal to a because a – 0 = a.
- Finally, (b – a) = 0 – a = -a. That is, (b – a) is the same distance from 0 as a, but has the opposite sign.
Looking across and synthesizing
You can raise one final discussion point: (b – a) and (a – b) are always on opposite sides of zero and the same distance from zero. In symbols this means (a – b) = -(b – a). But don’t worry too much about having your students use symbols for this expression. Instead, point out that if you know 8 – 3 = 5, then 3 – 8 is the opposite, or -5. This approach provides a nice way to make signed addition and subtraction easier.
6. FOCUS PROBLEM: Same Concept in a New Context
Distribute Handout #2.
Handout #2 Answer Key
This more focused problem gives teachers evidence of student understanding.
Project funding provided by The William and Flora Hewlett Foundation and S.D. Bechtel Jr. Foundation.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.