Rating Rate Plans
Sixth Grade Poster Problem:Expression and Equations
- Interpret and translate real-world situations into numerical expressions using variables.
- Write and evaluate numerical expressions involving whole-number exponents, variables, and specific values.
- Evaluate expressions with various values of their variables utilizing the Order of Operations.
- 6.EE.A.1, 2a, 2c
1. LAUNCH
- Per-text or per-minute charges
- Flat rate charges for a fixed number of text messages or call minutes per month.
- Overages and other additional charges and fees
- What is the “billing cycle?”
- How many minutes did this person use for calls? How were the charges calculated?
- How many text messages were sent and received? How were the charges calculated?
- How would you describe the type of plan this person has? Unlimited? Pay-as-you-go? Other?
2. POSE A PROBLEM
3. WORKSHOP
4. POST, SHARE, COMMENT
Poster A
Poster A displays three sample customers with different use patterns and lists the sums each should expect on the monthly bill. This group also provided a summary statement about the kind of customer who would benefit from the specific rate plan.
Poster B
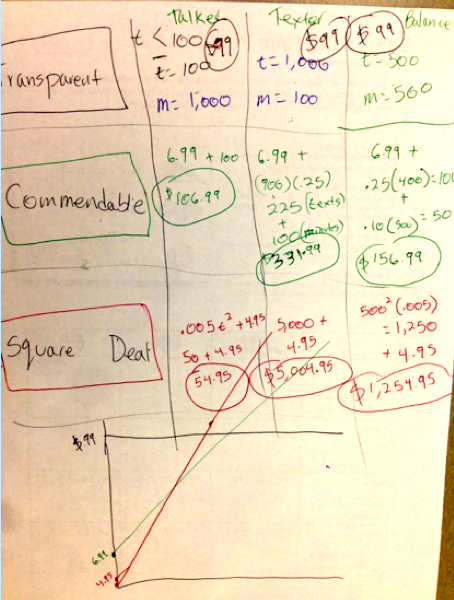
Poster B shows the work of the calculations and includes sample users who provide a much more dramatic difference in costs. They also made a preliminary attempt to display data as a graph. The graph is unlabeled, but is likely to be more illustrative than data-based. Notice that the graph for "Square Deal" is not curved.
Poster C
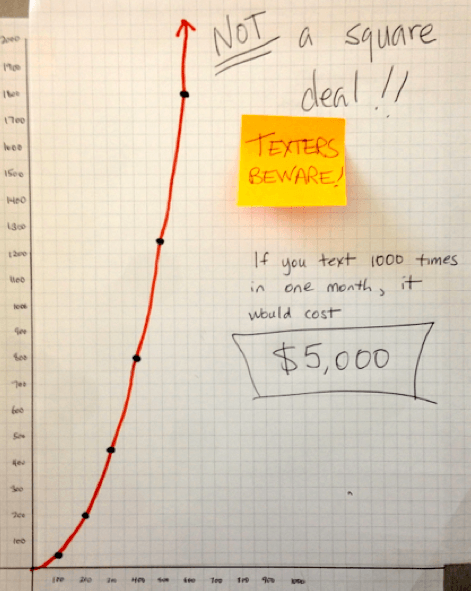
Poster C focuses on the skyrocketing of the texting charge with Square Deal’s rate plan.
Poster D
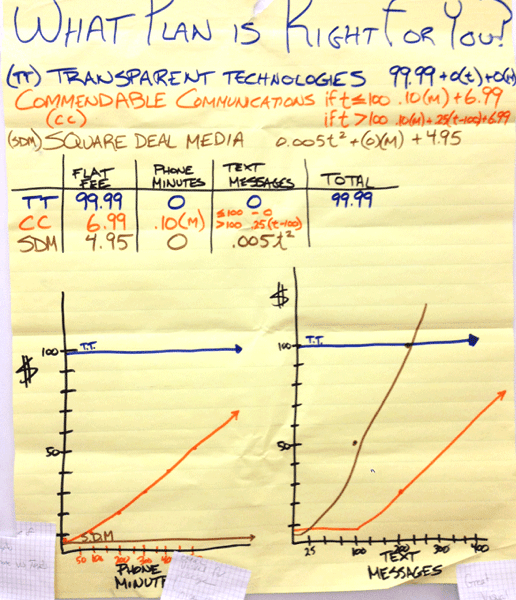
Poster D compares all three plans, showing the effect of increasing the number of minutes for a small fixed number of texts (left) and increasing the number of texts for a small fixed number of minutes (right). This shows ingenuity and understanding, even though the curve for Square Deal does not go up as fast as it should!
5. STRATEGIC TEACHER-LED DISCUSSION
6. FOCUS PROBLEM: Same Content in a New Context
- Food truck and restaurant prices differ.
- All the prices within a category are the same at each location.
Strategic Education Research Partnership
SERP Institute
1100 Connecticut Ave NW
Suite 1310
Washington, DC 20036
(202) 223-8555
Registered 501(c)(3). EIN: 30-0231116