Knowing Nets
Sixth Grade Poster Problem:Geometry
This problem is intended to open student’s imagination and to create a discussion on the main topics of the 6th-grade geometry standards: polygon area, prism volume, coordinate geometry, and nets of prism edges. This lesson plan begins with a discussion of geometrical nets, allows for the connection of geometry and Cartesian coordinates and extends the generalization of two dimensions to three-dimensional rectangular objects.
Downloadable Materials
This lesson also lays a foundation for the computation of Cartesian distances and for when the Pythagorean Theorem and square roots are introduced later.
Learning Objectives:
- Examine and identify nets and their properties and relate nets to solid figures.
- Determine lengths of figures by using a coordinate plane.
- Determine area measurements of rectangles and right triangles (composing and decomposing).
- Finding multiple nets for the same triangular or rectangular prism.
- Determine the volume of a triangular prism by comparing it to a rectangular prism twice its size.
Common Core State Standards for Mathematics:
- 6.G.A.1–4
Materials
- Scissors
- Tape
Teacher Tune Up:
1. LAUNCH
Show Slide #1
(a video clip of Kleenex box that is cut apart and flattened).
Ask students what they noticed about the video recording.
The box was flattened to become a net and then refolded to become a three-dimensional figure once again.
During the discussion, press for precise use of the following concepts:
- Dimensions
- Corner (Vertex)
- Edge
- Face
- Notice that “side” is not precise mathematical vocabulary in this context! A square has four sides, but a cube has faces that meet at edges and vertices.
Show Slide #2
(a still image showing the box as a three-dimensional shape). Have volunteers come up to the projected image and point to a corner (vertex), an edge, and a face.
Show Slide #3
(a still image showing the box as a two-dimensional shape - a net). Have volunteers come up to the projected image and point to a corner (vertex), an edge, and a face.
Have students turn to each other and talk about these questions:
- On a net, how can the same edge appear in different parts of the net?
- How can a corner appear on different parts of the net?
Encourage lively discussion, but do not attempt to settle these questions fully at this stage of the lesson.
2. POSE A PROBLEM
Show Slide #4.
Read the slide to the class. Make sure everyone knows what's being asked, then distribute Handout #1.
Handout #1 Answer Key
You may have the students work on the handout with partners. If students struggle or have no familiarity with nets, it is okay to allow students to use scissors to cut out nets to test. Consider how much time you would like to invest at this stage.
The purpose of this phase is the help students understand that there are certain properties of nets. Not all figures of six square units can fold into a cube, but many can. Encourage students build preliminary generalizations about what shapes are nets and what shapes are not nets and why.
3. WORKSHOP
As a warm-up to the workshop phase of this lesson, have students focus upon one of “Emile’s boxes” shown in Slide #5.
As you ask the following questions, write them on the board. Then write the answers with units as students give them. (Having the questions and answers for the simple cube visible will help students as they make their posters.)
- What is the length of an edge? [1 unit]
- What is the area of one face? [1 square unit]
- What is the total area of all the surfaces (surface area)? [6 square units]
- What is the volume of the cube? [1 cubic unit]
- Is this the only net for the cube? [no]
Say to your students: “During the workshop phase of this lesson, you are going to receive a handout with a net that is more interesting than Emile’s boxes. The challenge for your group is to figure out as much as you can about the figure and make a poster showing what you what determined. Be sure to display what you discovered and show how you discovered it.”
Distribute Handout #2—two copies to each group.
5. STRATEGIC TEACHER-LED DISCUSSION
As you begin the discussion, establish that the figure on the handout is indeed a net of a triangular prism. Then have various groups present their posters. Unlike in other “Poster Problems,” we haven’t defined “levels” students might rise through. Instead, help students connect the various concepts that appear in this activity. To that end, have groups show posters with examples of the various concepts below. Have students explain their thinking and connect concepts from various posters. Also point out posters on which students have already connected these ideas.
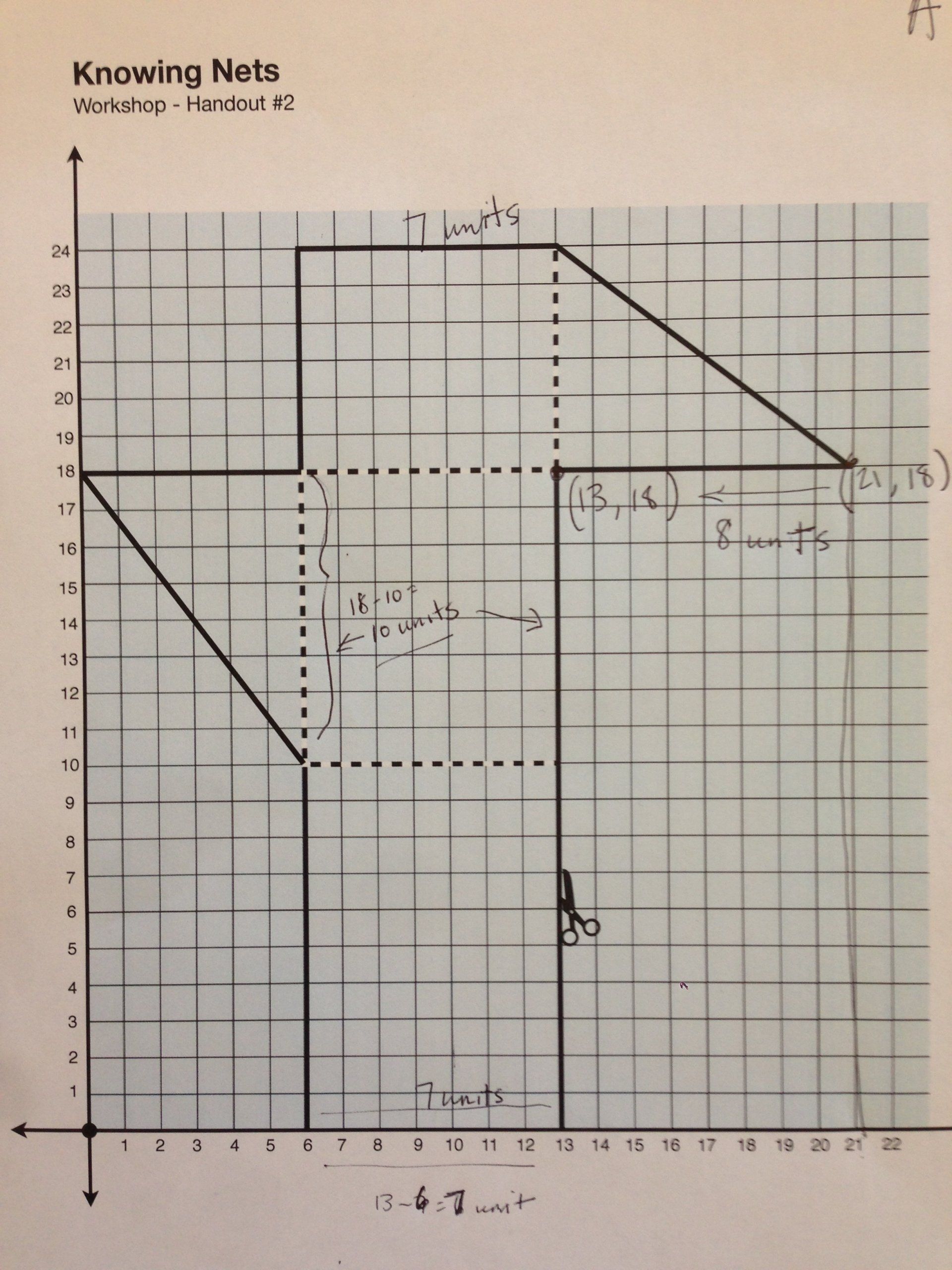
Concept 1: You can use a coordinate plane (or even just a grid) to locate and describe vertices, to determine edge lengths, and to compose and decompose shapes.
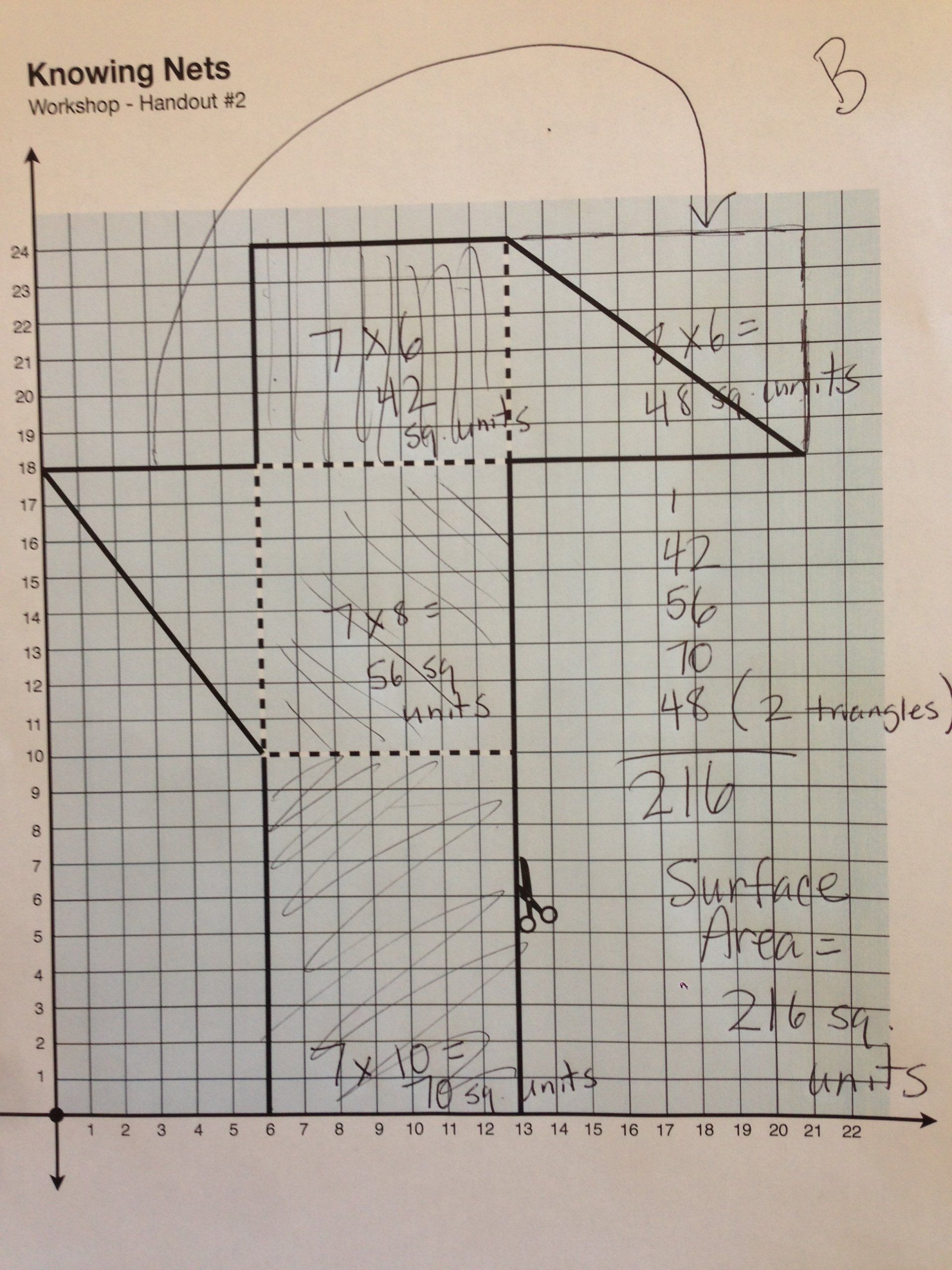
Concept 2: Area can be determined for each individual face using the net. The triangles can be doubled to make rectangles (area = l x w) and then halved to become triangles again. Logically, then, the area of the triangle equals 1/2(l x w). Caution: height of triangles are not always determined by one of the side lengths!
Concept 3: The surface area of the final prism is the total area of all the faces. A net helps make this clear.
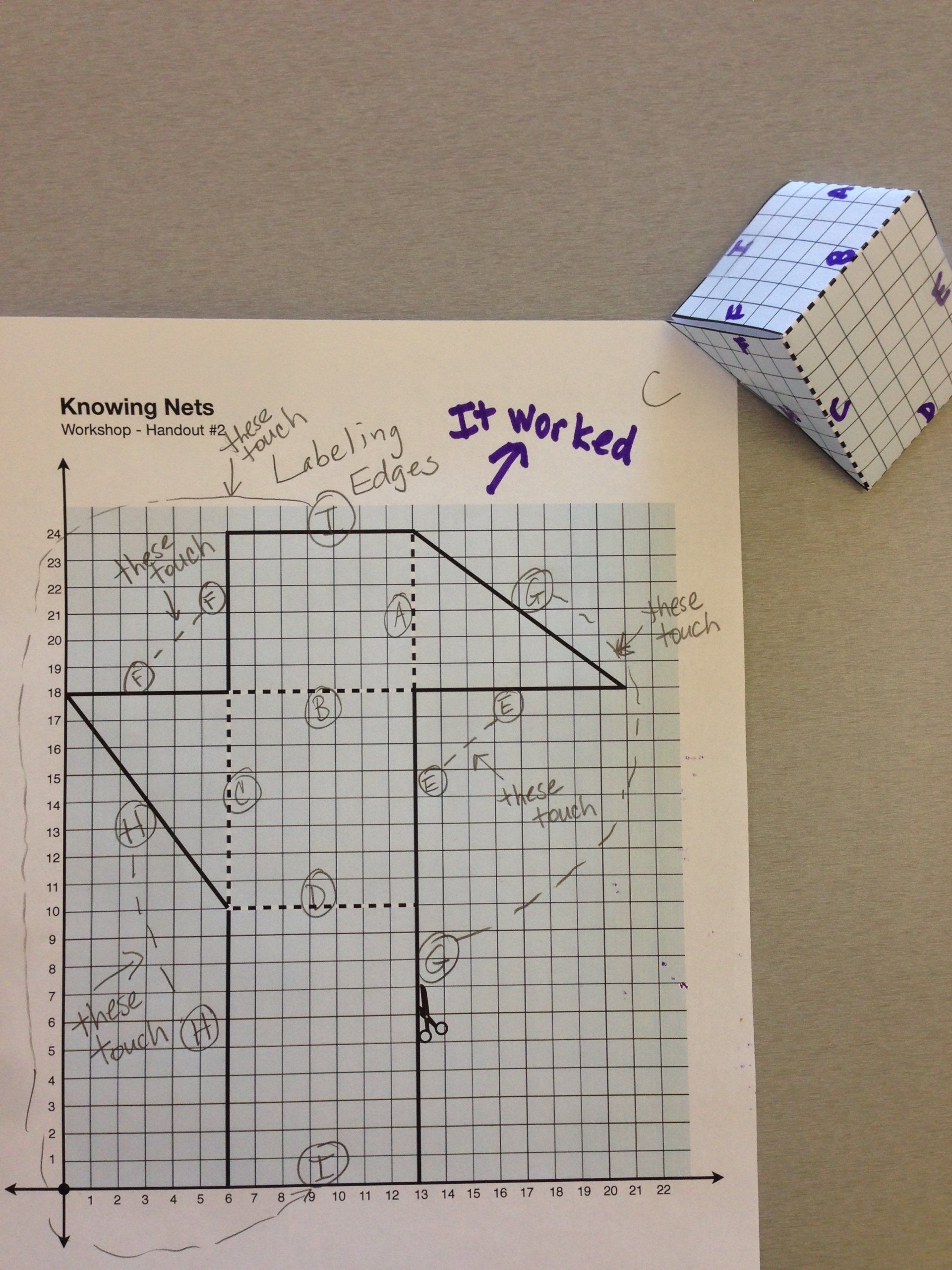
Concept 4: You can use the net to visualize and count edges. Some edges get folded and other edges get cut. Students can count the number of edges by changing the net into a solid or by thinking through how to count a cut edge if it joins with another edge. Some students might label or color-code corresponding edges.
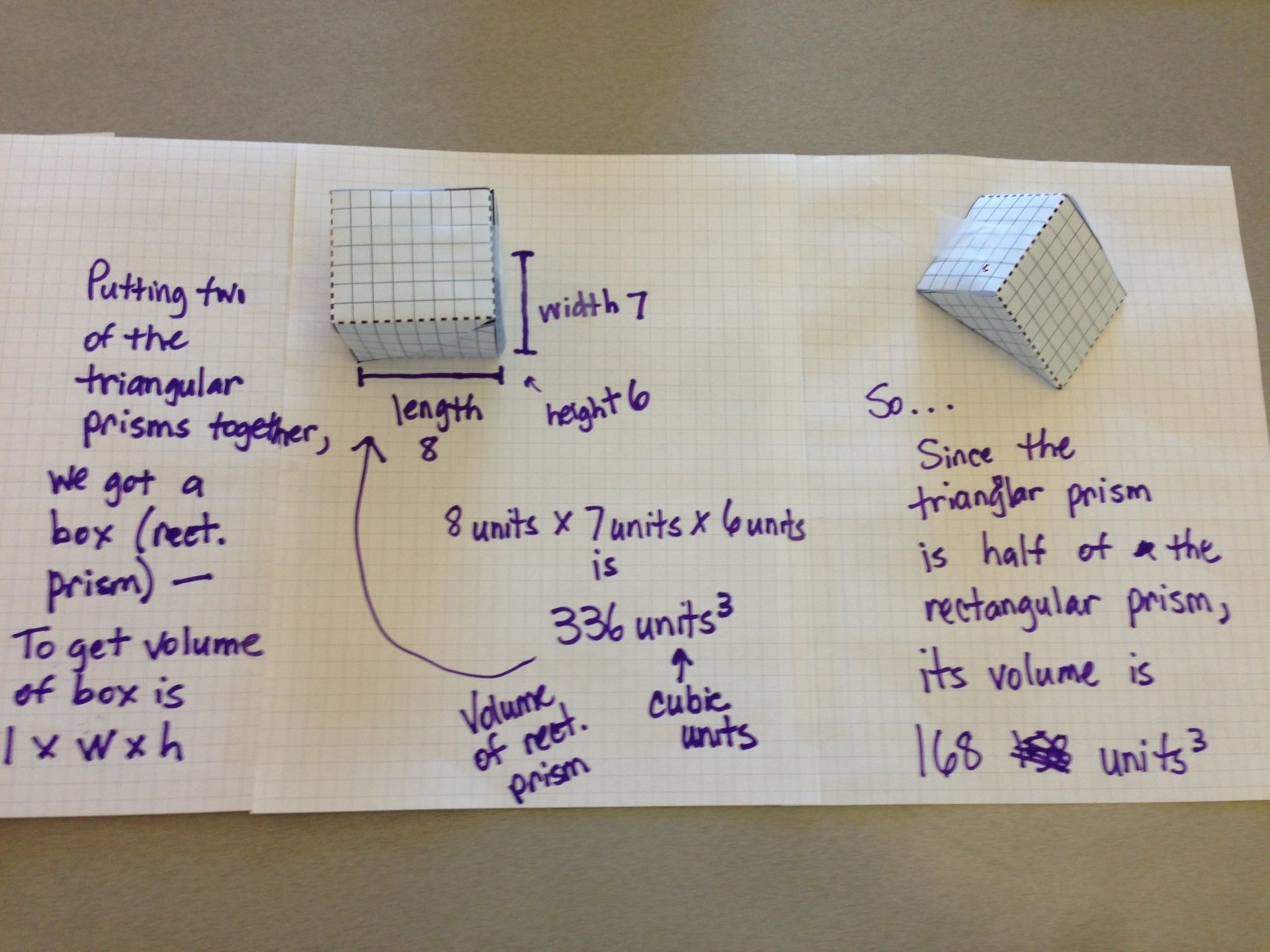
Concept 5: You can find the volume of this triangular prism by joining two triangular prisms together to create a rectangular prism. In Grade 6, students learn that the volume of a rectangular prism is found by multiplying length x width x height. Students can then use logic to determine that the volume of this triangular prism is half of the rectangular prism.
Concept 6: The exact same triangular prism can be made with nets that are shaped differently than the example given.
Additional Questions and Explorations
- What arithmetic do you do to find distances on a grid? [ subtraction ]
- What has to be true for that to work? [ the two places have to be on the same line ]
- What would you do to find a distance if they’re not on the same line? [ Students probably don’t know the Pythagorean Theorem—but they can tell things about the distance, e.g., it has to be more than the horizontal distance but less than the sum of horizontal and vertical ]
- What’s a good way to label edges so you can see which go together?
- How can you predict which go together without folding?
- What’s a reliable way to count the edges of a solid if you have the net? [ perimeter divided by two plus the inside “fold” lines ]
- What’s the maximum number of places a single vertex can appear on a net? [ varies, but for our nets it’s probably 3 ]
- Some nets don’t fold up into solids. What are some ways you can immediately tell a net is bad?
6. FOCUS PROBLEM: Same Concept in a New Context
Distribute Handout #3.
Handout #3 Answer Key
You can present this task in a range of ways, from a homework assignment for individuals to another group task.
Here the challenge is to draw a net that corresponds to a picture of a rectangular prism. There are number of correct ways to draw the net associated with the solid pictured on the handout. Focus students’ attention on creating an accurate representation of the dimensions and edges. Students can go on to do determine surface area and volume.
Project funding provided by The William and Flora Hewlett Foundation and S.D. Bechtel Jr. Foundation.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.