Seventh Grade Poster Problems
Drag Racer Dragonfly
RATIOS AND PROPORTIONAL REASONING
Aligned to CCSS Seventh Grade Standard 7.RP - 1, 2a, 2b, 2c, 2d
The tasks in this lesson give students the opportunity to work with situations that represent three types of rate problems: a) How long? In this situation, students need to determine how long it takes the dragonfly to fly a specific distance; b) How far? Here, students need to find the distance the dragonfly flew in a given time; c) How fast? In this case, students must figure out the rate at which the dragonfly is flying.
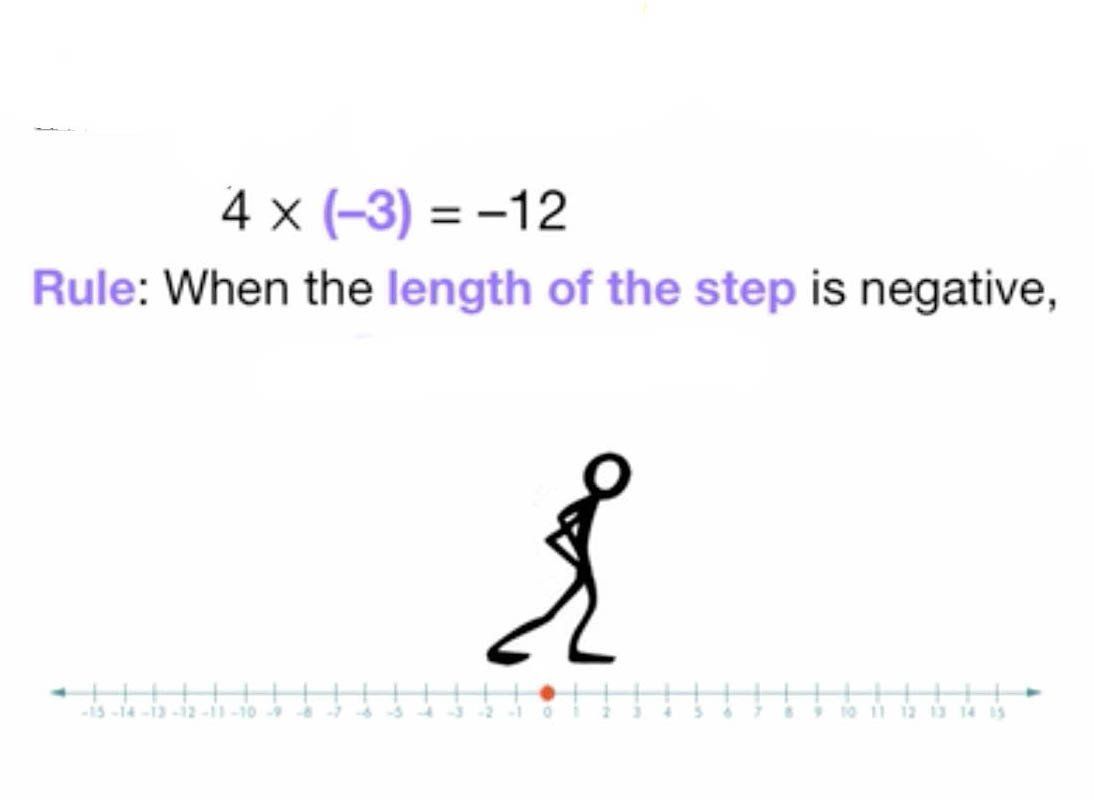
Seeing Sums
THE NUMBER SYSTEM
Aligned to CCSS Seventh Grade Standard 7.NS - 1 a, b, c, d
Unlike other poster problems, this problem is about mastering a mathematical model, the number line model for sums, rather than using the model to solve a “real life” problem. The model will provide a context for sparking a discussion in which your students will use language and reasoning skills highlighted in the CCSSM. In the launch, you can first set the stage by asking students to consider limitations of the familiar set model for sums and differences. Then, you can introduce the number line model with a short animation. Next, the students explore the model, first by hand, and then with a dynamic number line game. Finally, in the concluding discussion, you will use the model to elicit key ideas from your students.
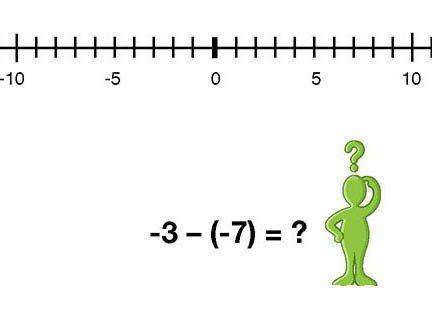
Walking the Line
THE NUMBER SYSTEM
Aligned to CCSS Seventh Grade Standard 7.NS 2a
The Number System standards in grades 6-8 build on the grades K-5 standards related to Number and Operations in Base Ten as well as the Fractions strand from grades 3-5. In the 6-8 Number System standards, students are expected to reason about and compute with rational numbers, which include integers (positive whole numbers, 0, and negative whole numbers) as well as decimals that terminate or repeat, and fractions.
This problem leads students through a sense-making activity that helps them think through why a negative times a negative is a positive.
On the Download
EXPRESSIONS AND EQUATIONS
Aligned to CCSS Seventh Grade Standard 7.EE - 4a
When you download movies, games, or other items with a large amount of data to your phone, the download process may take a long time to finish. But how long, exactly? This problem uses cell phone download speeds as a context for setting up and solving linear equations. The mathematical goals are to solve equations for a specific value and to represent a delayed start time meaningfully.
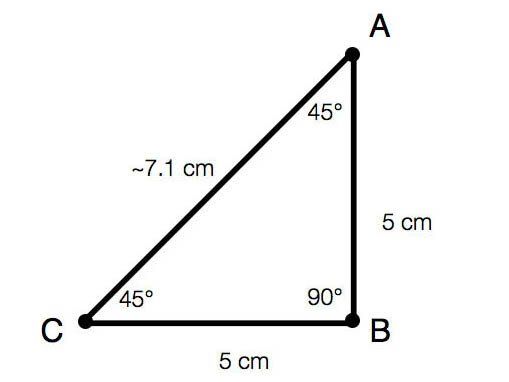
Triangles to Order
GEOMETRY
Aligned to CCSS Seventh Grade Standard 7.G 2
In this poster problem, students try to build triangles based on specific criteria. These could be side lengths, or angles, or a combination of both. Students get experience constructing triangles based on “conditions,” for example, when they know some angles and side lengths. They go on to generalize, and develop understanding about when you can determine a triangle from partial information and when you cannot.
Try, Try Again...
STATISTICS AND PROBABILITY
Aligned to CCSS Sixth Grade Standard 7.SP 5–8
In this problem, students get experience with both theoretical and empirical probability for compound events; that is, situations where something happens more than once, and you’re trying to find the probability of a particular combination of results.