Walking the Line
Seventh Grade Poster Problem:The Number System
The Common Core Mathematics Standard 7.NS.2a contains several key ideas. One major conceptual milestone students must pass in meeting this standard is understanding why (-1)(-1) = 1. The proof of this identity relies on the distributive property of multiplication over addition (see the Teacher Tune-up links for more explanation of the proof).
Downloadable Materials
While the proof shows that (-1)(-1) = 1, it might not help your students develop a feeling for why this fact is true. This activity uses a familiar model, the number line, to develop an intuitive feeling for why it makes sense to define (-1)(-1) = 1.
Learning Objectives:
- Understand that the rules for multiplication can be extended from whole numbers to include negative numbers.
- Use a model to develop an intuitive understanding of why (-1)(-1) = 1.
Common Core State Standards for Mathematics:
- 7.NS.A.2a
Teacher Tune Up:
About Models of Multiplication
This lesson uses a number-line model of multiplication. You take a number of steps, and each step is so many units long. The total distance is the product of those two numbers. We model negative numbers in this situation by facing in the negative direction, by walking backwards, or both (see the slides for details). We hope this model will make sense to students, and help them see that if they face backwards, and step backwards, they move forwards: a negative times a negative is positive.
Number Lines
Number lines in Grade 7? You bet. They are a clear model of the entire number system, not just a tool for multiplication. They also help students prepare for further math: first, they’re the one-dimensional analog of the all-important Cartesian plane. If you can’t navigate a number line, you are sure to get lost on the plane. Secondly, our model for addition (and multiplication as repeated addition), often using arrows, mimics what students will see later when they study vectors. This leads, eventually, to understanding complex numbers and linear algebra.
1. LAUNCH
Preparation: Before class starts, use painter’s tape to make a large number line on the floor of your classroom. Arrange the students’ desks so everyone can see the line. Set up the line so positive numbers are to the RIGHT from the students’ point of view. The number line should go to at least ±12. Going to ±15 will match the upcoming handouts.
Start with an introduction:
“In today’s class we are going to look at a model for multiplication based on walking on a number line. Luckily we have a life size number line right here on the floor! Notice that 0 is in the middle, positive numbers are to your right, and negative numbers are to the left.”
“Let’s start with an example. How can we model 3 × 2 using our number line?”
Some students might say to start at 6. While it is true that 3 × 2 = 6, we do not want to jump to the answer 6 right away. Instead, ask students how we might start at 0 and walk along the life-size number line to model 3 × 2 = 6. Take ideas from students. Focus on the idea of taking 3 steps each with a length of 2 units. Model for the students that you can start at 0, face the positive direction, and take 3 steps of 2 units each. In the end you will land at 6. This is one way to represent multiplication sentences: as number line walks.
Show Slide #1
(video).
Work with students to define the model:
“To make this a walking model, the walker starts at 0 facing the positive direction “by default.” Then follow the conventions for number or steps and step lengths.”
Ask: "What is a step?" [for consistency, define this as a single step using one foot]
Ask: "How can steps differ in length?" [some people take long steps, others take short steps]
Ask: "How can we represent these different-sized steps on our life-sized number line?" [use the intervals on the line, so a step length of 3 covers 3 intervals on the number line]
Ask for a volunteer to “act out” 4 × 3 = 12.
You can tell students that even though we “know” the answer to 4 × 3 = 12, we are going through these steps carefully because things are about to get more interesting.
Show Slide #2
(video).
“Here’s an example where things can get more challenging. What happens when we try to model the multiplication (-4) × 3? To make the model work, we will need to incorporate the –4 into our walk. Let’s make this rule:
“When the number of steps is negative, the walker first faces in the negative direction and then walks normally.”
Have a student do this walk on your life-size number line.
Show Slide #3.
Next, we need to think about the case of a positive times a negative number when the positive number comes first. What could 4 × (–3) mean in our model?
When the step length is negative, we have to step by a negative distance. In other words, we step backwards.
Have a student do the walk 4 × (–3) = –12 on the life-size number line. Be sure to emphasize the difference between this walk and the previous walk. [In this case, the student is facing forward and stepping backward.]
Show Slide #4
(video).
Now for the strange one: What do we do if we have (–4) × (–3)? What does our model say?
Have students figure out what happens when they incorporate both rules:
When the first number is negative, you have to face negative.
When the second number is negative, you step backwards.
Slide #5
(video) demonstrates how this makes the walker move in a positive direction, showing that (–4) × (–3) = +12.
Make sure students are comfortable with the model. It might be worth the time to allow several different students to try new walks on the number line. While the number line walker is making a walk, his/her classmates can help by reminding them how the parts work. They can also make predictions of where the walker will end up.
Once students feel comfortable with the model, they will use it to model some multiplication problems on paper.
2. POSE A PROBLEM
Students should work with a partner on Handout #1.
Handout #1 Answer Key
Debriefing:
Discuss with students how they dealt with (g) and (h)—the ones with addition. Note that you can add before or after the multiplication. If you add before, it’s kind of the same as starting at a different place than zero. But it’s also like taking a single step that might not be the same as the one in the multiplication.
Solutions:
a) Face right (positive), five steps of length three.
b) Facing right (positive), three steps of length five.
c) Facing right (positive), take two steps backwards, each of length three.
d) Turn to face left (negative); take two big steps (forward) of five each.
e) Facing left, take seven steps backwards, each length two.
f) Facing left, take two steps backwards, each of length four. You land at +8.
g) Facing right, take two steps back of length three (to –6), then jump forward 10 to +4.
h) Face right and go two to +2. Then face left (negative) and take six steps backwards of two each (+12) to land at +14.
IMPORTANT: Allow the pairs of students to model each of these solutions by walking the line themselves. Walking the line is a powerful way to check answers and to experience how this model “feels.”
Extension:
Have students make up number sentences for each other. Ask what makes an interesting number sentence.
3. WORKSHOP
Put students in pairs or groups, and give them Handout #2.
Handout #2 Answer Key
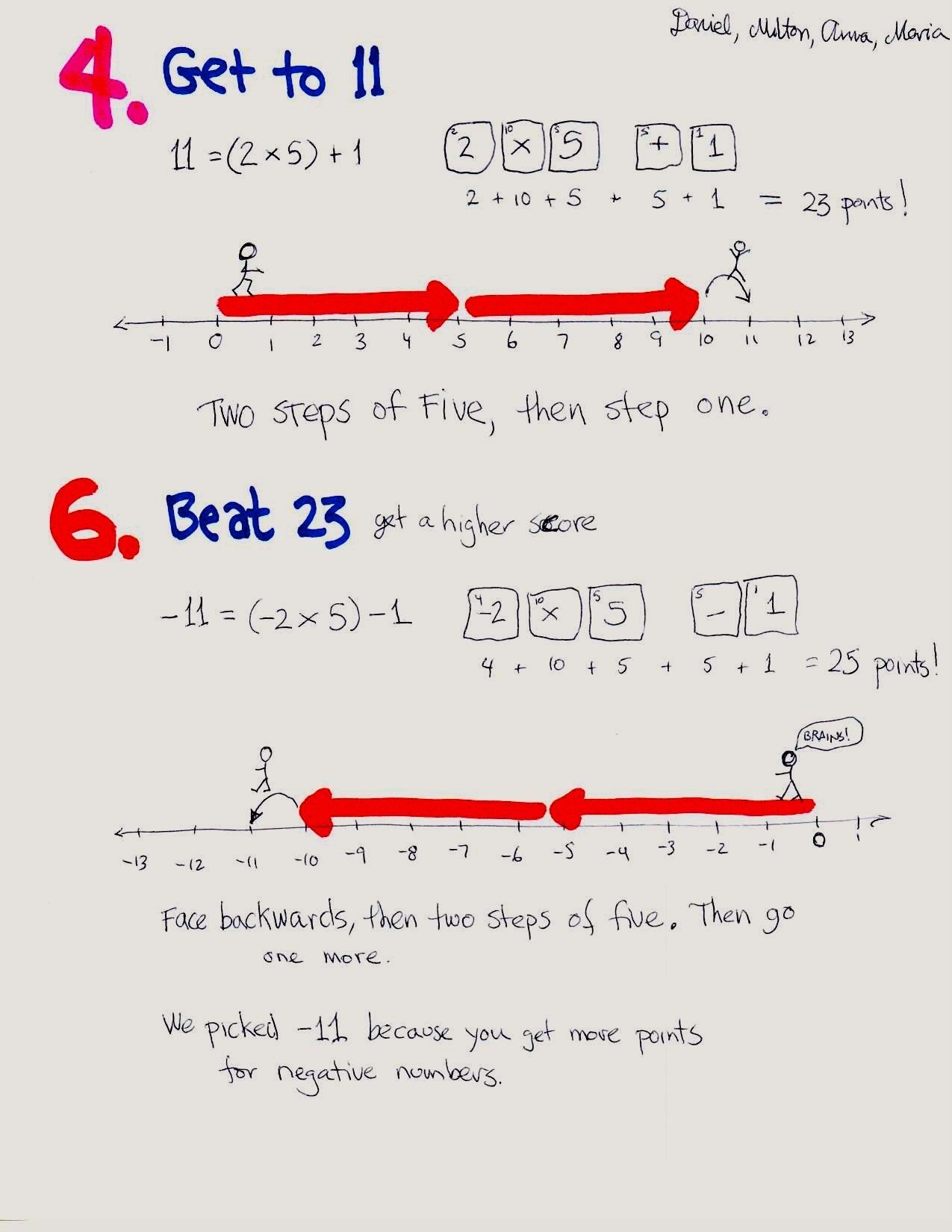
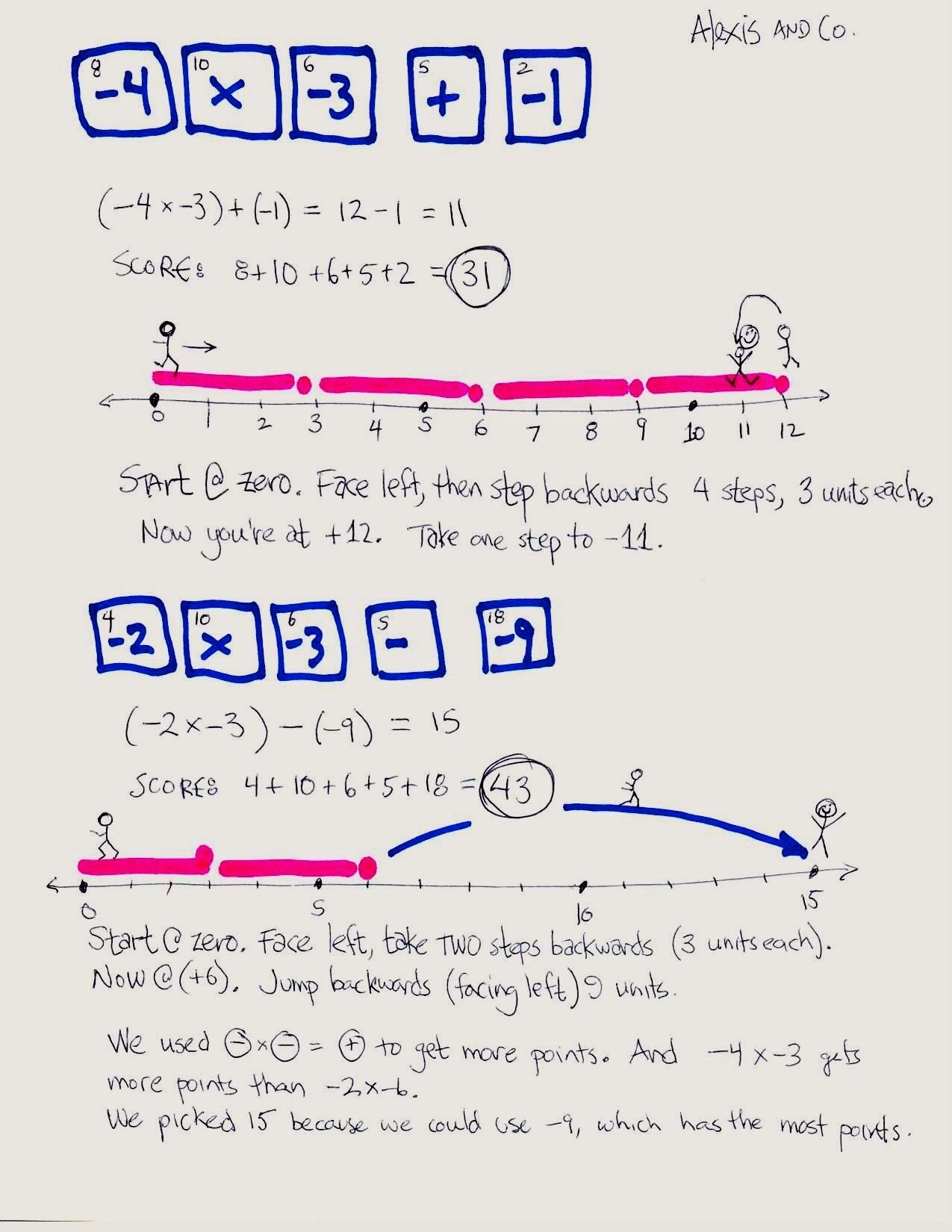
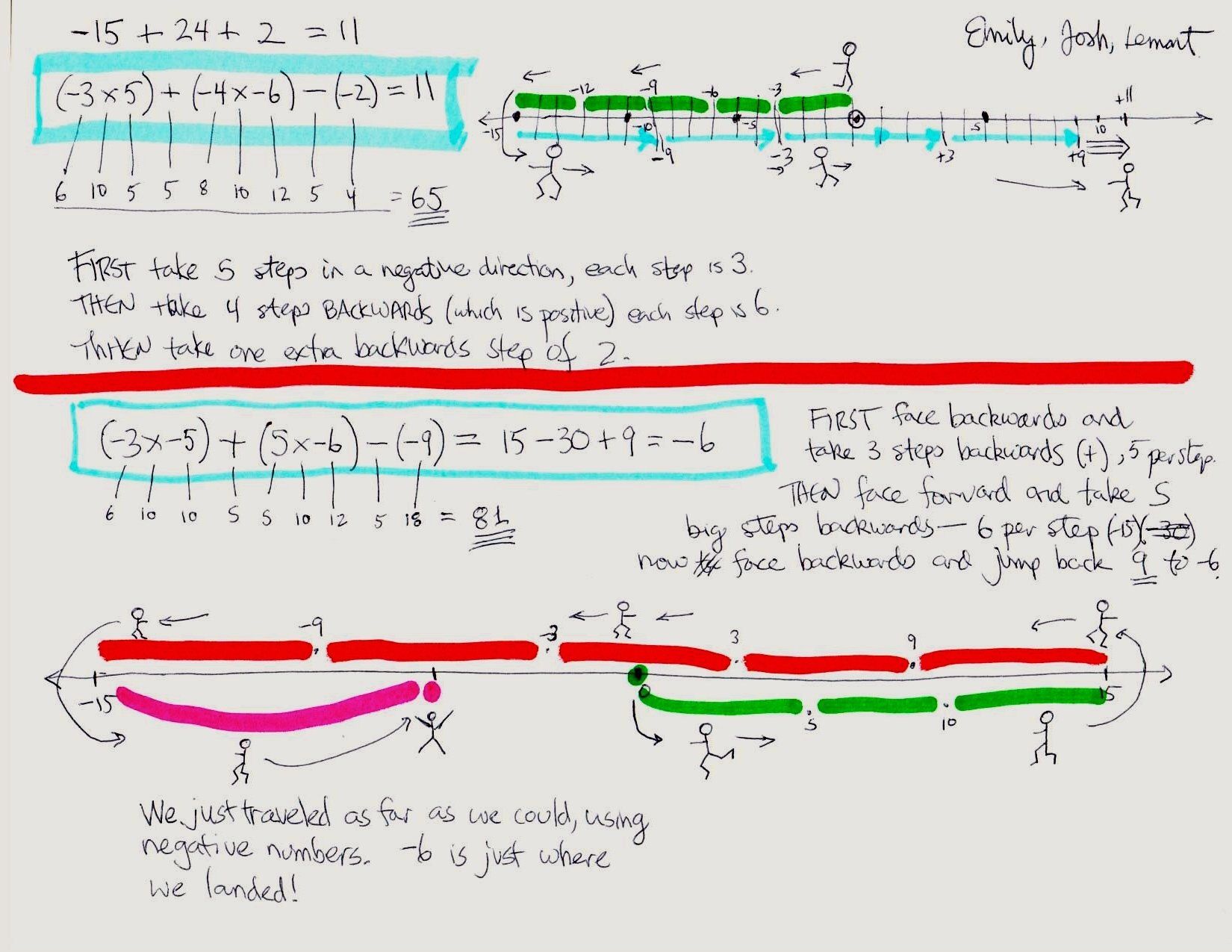
For their posters, each group is to make one number sentence ending in +11, and another ending in a number they choose in the interval from –15 to +15. In addition to writing the number sentence, they should draw the “walking path,” explain it in words, find the score, and be able to act it out on the class number line.
Students should also tell why they chose that number.
“Scoring” the expressions:
Each numerical expression gets a score. Find the score by adding the scores of the “tiles” used to make the sentence. Students don’t need to cut the tiles out, but the tiles limit what students can do. For example, there are no ones or zeros, and only one of each other number.
For operations, groups get one plus, one minus, and two multiplication signs.
Students may reuse the tiles when they move on to another number sentence.
Notice that negative numbers score more than positive; this means that students who are willing to use negative numbers might get a higher score.
Show Slide #6.
FYI:
- An example of a high-scoring sentence is (–3 × 5) + (–5 × –6) = 15, for a total of (6 + 10 + 5 + 5 + 10 + 10 + 16) = 62 points. That is not the highest-scoring possibility for 15.
Note on negatives:
- If students try to put negative numbers together to make subtraction, applaud their ingenuity. Unfortunately, it breaks the ”you may not put two numbers next to each other” rule.
- This rule keeps students from making –8 by making the math equivalent of a run-on sentence, e.g.: –8 × (6 -2 -3) + (9 -5 -4)
- Technically, this hangs on the distinction between using the minus sign for the opposite of a number (i.e., as a unary operator) and using it for subtraction (a binary operator). That’s too obscure for most students, so just explain they have to find another way.
(This rule also means that the maximum possible number of tiles you can use in a sentence is nine.)
5. STRATEGIC TEACHER-LED DISCUSSION
Facilitate a discussion of the different approaches. Select a sequence of posters to use that will help students move from their current thinking (Levels 1–2) up to Level 3 or 4.
Level 1:
Students create only straightforward calculations such as –2 × 4 = –8 and 2 × 5 + 1 = 11. No obvious attempt to use negative numbers to get a higher score.
Level 2:
Students might add a negative instead of a positive in order to get a higher score, e.g., 2 × 7 + (–3) = 11. That is, there’s some attention to getting a higher score, but no ingenious use of multiplication. Students might also include an additional operation to get a higher score, e.g., 2 × 9 + (–2) – 5 = 11. Or they might subtract a negative to get a positive result, e.g., –4 – (3 × –5) = 11.
Level 3:
Students multiply two negatives together in order to make a positive number, e.g., (–2) × (–7) + (–3) = 11.
Level 4:
Students find ways to go long distances in their walks, for example, by changing direction.
An example is (3 × (–3)) + ((–4) × (–5)) = 11. This approach shows that they recognize that larger numbers (positive or negative) give higher scores, so it’s an advantage to go in the opposite direction first so they can come back over a greater distance.
The task where students choose their own goal-number and explain the reason is particularly telling. There, the astute student will pick a large positive or negative number in order to have a longer distance to travel. As a further refinement, students might see that they score more if the two factors are quite different. For example 5 × 6 = 30, which scores 21: (5 + 10 + 6). But 9 × 3 = 27 (a smaller product) scores 22: (9 + 10 + 3). Of course, –9 × –3 scores even more!
Questions to ask across presentations:
- If you had no parentheses in your expression, would it still be right? (Probably, because of order of operations.)
- Why did you use negative numbers here instead of positive? (To get a higher score.)
- Why do you suppose this activity is set up with higher scores for negative numbers? (To get students to use negatives.)
Finally, close the discussion by filling in Slide #7.
6. FOCUS PROBLEM: Same Concept in a New Context
Distribute Handout #3. Have students work individually or in pairs.
Handout #3 Answer Key
The tasks here are straightforward, but highlight some deep mathematics. First, they ask students to think about the properties of all the points on the plane: of all the points, which have a positive product of their coordinates? This is actually the same idea as for all of graphing: when we graph y = 3x + 1, say, we’re shading all the points on the plane where that is true.
Second, we ask students where the product is zero. This is good thinking practice for understanding what an intercept means (that one of the coordinates is zero) and for understanding the all-important zero-product property that comes into play in a big way in algebra.
Answers
- Answer vary, but students should have points in all four quadrants.
- Products should be correct. Pay special attention to the signs.
- The first and third quadrants should be shaded. Note that students do not have to know the numbering of quadrants—but this might be a good time to introduce that system.
- The upper-right quadrant has x and y both positive, so x times y will be positive. In the lower left (quadrant III) both x and y are negative, so all of its products are positive no matter which point you choose in the quadrant. The other two quadrants mix positive and negative, so their products are negative.
- Students should highlight both axes.
- The products are zero on the axes—and only on the axes—because being on an axis means that one coordinate is zero, and zero times any number is zero.
Project funding provided by The William and Flora Hewlett Foundation and S.D. Bechtel Jr. Foundation.
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.