Triangles and Constraints
Standard 7.G.2 reads:
Draw (freehand, with ruler and protractor, and with technology) geometric shapes with given conditions. Focus on constructing triangles from three measures of angles or sides, noticing when the conditions determine a unique triangle, more than one triangle, or no triangle.
What does this mean? If you had just taught a traditional high-school geometry course, you’d recognize immediately that this leads to understanding triangle congruence and similarity; it’s the foundation of a number of bread-and-butter theorems such as SAS, ASA, SSS, and hypotenuse-leg, as well as the “gotcha,” SSA, which does not work in general.
At grade 7, then, we want to prepare students so that by the time they study these theorems, they will have had relevant experiences, and will have developed some intuition about how the sides and angles of triangles interact.
If you have not recently taught high-school geometry, or feel a little shaky about why SSA doesn’t work, we’ll cover all that here as well.
What does it mean to determine a “unique” triangle?
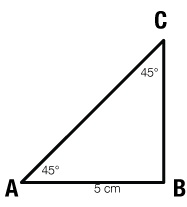
Standard 7.G.2 (above) includes a tricky phrase: "noticing when the conditions determine a unique triangle." Let’s build up an example that will illuminate much of what follows.
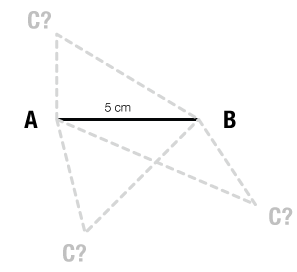
Suppose Penelope is trying to get us to draw a particular triangle, and has to talk to us on the phone. No drawing, no pictures.
“It’s triangle ABC,” she says.
But this is of little help; we could label any triangle ABC.
“AB is 5 centimeters long.”
Now we’re getting somewhere. We draw AB as a segment 5 cm long. Now part of the triangle is all set. But we know nothing about where point C is. It could be anywhere!
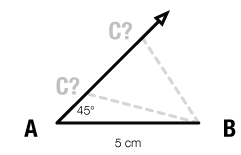
Penelope continues: “The angle at point A—let’s call it angle A, or ∠A—is 45°.”
Now we can construct a 45° angle at point A. We build it so it extends up and to the right. Now we know that point C is on that “ray,” but we still don’t know where. We have countless possible triangles.
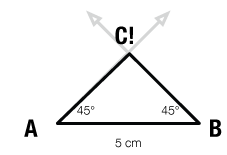
We tell Penelope we still need more information. She says, “Angle B is also 45°.”
We draw the ray from B, and it intersects the “A-ray” in just one point. It must be point C.
We’ve been given three conditions:
AB is 5 centimeters
∠A is 45°
∠B is 45°
And with those, we can draw Penelope’s triangle reliably. The conditions specify a unique triangle.
Wait—Three numbers?
It’s interesting that we completely specify the triangle with three numbers. We might think that it would take six numbers to specify the triangle:
- the three side lengths and the three angles; or
- the x and y coordinates of the three vertices.
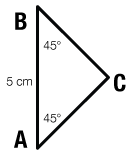
And it might—depending on what you mean by unique. For example, here’s a different triangle ABC. It also has a side length of 5 cm and two 45° angles. If Penelope saw it, she would say, yeah, that’s my triangle.
The triangle is not completely the same—the coordinates of all the points are different, it’s lower on the page, and it looks rotated and reflected—but it has all the same side lengths and angles. And that tells us what we mean by unique: that if we follow the instructions, all of the triangles we get will have the same 3 side lengths and 3 angles. When we only had one or two conditions, we could make lots of triangles, but they would be fundamentally different.
The official word for this is that all the triangles we get will be congruent to one another. We often describe congruence as, “they have the same size and shape,” or “if you cut one out, it will exactly cover the other.”
In this case, the three numbers determined the triangle. Oddly enough, this means Penelope can now give bad information. For example, suppose she told us that angle C was also 45°. That’s impossible! We know it’s 90°! Correct. If you get too much information, it could create a contradiction. We will try hard to avoid letting that happen to our seventh-graders—but stay alert.
Do three numbers always determine a triangle?
No. And that’s the more advanced part of the lesson.
Let’s back up a bit: there are six possible numbers we’re interested in: the three side lengths and the three angles. Imagine a board with six slots (shown). We put numbers in the slots one at a time.
- With one number—side or angle—we can make lots of different triangles.
- With two numbers, in any combination, we can usually make lots of triangles.
- With three numbers—well, it depends.
Our example was a situation with one side and two angles. Importantly, the two angles we knew were on either end of the side we knew. Angle A and angle B are adjacent to side AB. This is the ASA (angle-side-angle) situation in high-school geometry, though we want students to come to their own understanding without relying on somebody else’s labels for now.
We might also have had one adjacent and one opposite angle. Suppose we knew AB was 5 cm, and ∠A and ∠C were both 45°. Angle C is across from AB, so it’s the opposite angle. And that fundamentally changes the triangle.
This triangle is the same shape as the former ABC, but it’s bigger. If we fill in the numbers, we see that this triangle can’t have the same side lengths: AC is more than 5 cm here, but it was clearly less than 5 cm in the original triangle ABC.
Still, the three numbers (two angles and one side) again determined the triangle. And there are no other ways to arrange two angles and one side.
Does that mean that you can always determine a triangle if you pick two angles and one side? No! Suppose the two angles were 90°. You can’t make such a triangle.
Four Situations
When you think about it, there are really four types of situations for three numbers:
- Three sides.
- Two sides and one angle.
- Two angles and one side (that’s what we just did).
- Three angles.
And all of them have special conditions to be able to make triangles at all, or to determine a triangle uniquely. At this point, I’m going to tell you the “answers,” but if they’re not familiar, you should play with the materials in the poster problem Triangles to Order, and make triangles until it’s obvious why the following is true.
Three sides. These determine a triangle, provided they satisfy the triangle inequality. Having said that, it’s not easy to construct the triangle without using a compass (and that would be asking too much in Grade 7). Kids should guess and check and just do their best.
The triangle inequality says that, to have a triangle, the longest side must be shorter than the sum of the other two sides. So, for example, you cannot make a triangle with side lengths 1–3–5.
Two sides and one angle. If the angle is between the two sides (SAS) you definitely get a triangle every time. This is the easiest way for confused students to see how a whole triangle is determined by three numbers.
If the side is not between the two angles (SSA; avoid calling it ASS for obvious reasons) you get zero, one, or two triangles. In the “one” condition—a unique triangle—the “other” angle is 90° and the two sides are the hypotenuse and a leg. This is the subtlest of all the possibilities; do not expect all students to get this!
Two angles and one side. This is what we did with Penelope, above. As long as the angles add up to less than 180°, you get a unique triangle. Having said that, the ASA situation is easier to construct than SAA. (If you know that the sum of the angles is 180°, though, you can compute the other angle in the SAA situation and get the easy ASA again.)
Three angles. First, the sum has to be 180°. And in that case, you get similar triangles, not congruent ones. That is, you can have an infinite number of triangles, all the same shape, with the same set of 3 angles. But they can all be different sizes. No unique, same-shape-same-size triangles.
Two angles and one side. This is what we did with Penelope, above. As long as the angles add up to less than 180°, you get a unique triangle. Having said that, the ASA situation is easier to construct than SAA. (If you know that the sum of the angles is 180°, though, you can compute the other angle in the SAA situation and get the easy ASA again.)
Three angles. First, the sum has to be 180°. And in that case, you get similar triangles, not congruent ones. That is, you can have an infinite number of triangles, all the same shape, with the same set of 3 angles. But they can all be different sizes. No unique, same-shape-same-size triangles.