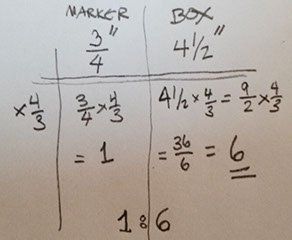What's the difference between a ratio and a fraction and why should I care?
Most important:
a ratio describes a proportional relationship, and a fraction is a number. We use fractions a lot for computations with ratios, but on their own, fractions are just numbers.
Next: ratios are the things with colons. When you cook (regular long-grain white) rice, you might use a 2:1 ratio of water to rice. We say, “two to one,” and we mean two parts water to one part rice. Fractions look like, well, fractions.
Ratios can have more than two items. You might make trail mix in a 1:1:1 ratio of nuts to raisins to chocolate chips. If you want more raisins per handful, you could change that ratio to 2:3:2.
Rules for Ratios
There’s really one rule: if you multiply (or divide) each of the numbers by the same factor, the ratio stays the same. So the 2:1 rice ratio is also a 4:2 ratio or a 10:5 ratio. We haven’t assigned units to those numbers, either, so the 2:1 might be cups and the 10:5 might be tablespoons. Or liters.
If one of the numbers is a “1,” it’s a unit ratio, which is closely related to a unit rate. The rice ratio of 2:1 is a unit ratio but 4:2 is not. We could have a different unit ratio: 1:½, but to a math person that sounds a little weird. We’d usually express it as 2:1.
When it Gets Tricky
If you can interpret the numbers in the ratio as parts or wholes, you have to be careful about part:part and part:whole relationships.
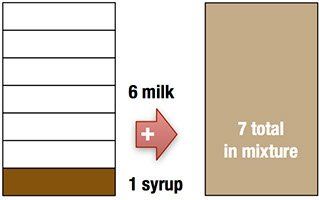
Suppose we’re making chocolate milk and use a 6:1 ratio of milk to chocolate syrup. (That’s more intense than most chocolate milk.) What fraction do we use to express that ratio?
It depends what question we’re asking, and what we’re doing.
If we want to know how much syrup to add to a quart (four cups) of milk, we should use ⅙. We’ll take ⅙ × 4, and get ⅔ of a cup of syrup. (This is part:part.)
But if we want to know how much syrup there is in a cup of chocolate milk, we use ⅐. This is because when we add syrup to milk, the total amount of mixture increases. In this part:whole relationship, the “whole” gets bigger.
In another example, suppose the ratio of boys to girls at a concert is 2:3.
What fraction of the audience is boys? ⅖. Not ⅔. But suppose we knew there were 900 girls, and wanted to know how many boys were attending? Now we use ⅔, and calculate ⅔ × 900, or 600 boys.
A good exercise for yourself is to figure out a question that would use a fraction made of any possible combination of the three numbers (in this case, 2, 3, and 5). For example, what question would use 5/3? (720 girls attended the next concert. How many people attended altogether?)
When It’s Not Tricky
The problem of deciding what number to use goes away when it’s not a mixture problem—not a part-whole situation. For example, suppose the ratio of the height of an object to the length of its shadow is 3:2. The flagpole’s shadow is 24 feet long. How tall is the flagpole? That’s (3/2) × 24, or 36 feet.
Notice that in this situation, putting a “5” in the denominator doesn’t make any sense. Why not? Because we never combine the flagpole and its shadow the way we put the syrup and milk together (to make seven units of chocolate milk), or the way the boys and girls all attend the concert. So we never add the two and the three.
(Students can still get confused between additive and multiplicative strategies. For example, suppose the flagpole problem begins by saying that Dr Markov—who is 6 feet tall—has a shadow that's 4 feet long. The school flagpole's shadow is 24 feet long. How tall is the pole? The right, proportional answer is 36 feet, using that 3:2 ratio. The wrong, additive answer is 26 feet, assuming the rule to be, "the shadow is 2 feet shorter than the object." That's a different issue from the part-whole decision whether to add the numbers in the problem.)
Using Ratios to Help Students Understand
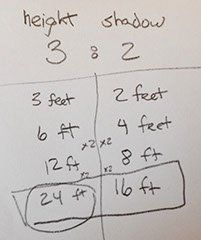
Calculations with fractions can frighten students. They look complicated and abstract. Sometimes, taking a step back and making a ratio table can help. In a ratio table, each row has to be a multiple of the top row, which holds the “basic” ratio. This table below shows work on the flagpole problem we described earlier. However, this student doesn’t understand how to multiply by 3/2:
In each row, the student consistently multiplied the previous row by 2. He or she found that if the shadow is 16 feet, the height must be 24 feet.
It’s also true that the relationship holds if you add two rows. So (adding the first and last rows) if the shadow were 18 feet (16 + 2), the flagpole would have to be 27 feet (24 + 3).
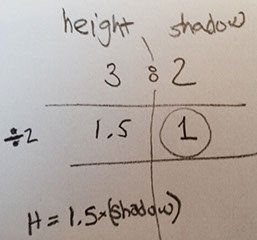
Students can use a fraction table to find a unit rate. They operate by multiplying (or dividing) in order to get “1” in the ratio. Here is different work on the flagpole problem:
Here the student found that the height is 1.5 times the shadow, and even wrote a formula. With that formula, anyone can calculate the answer to any height-and-shadow problem with a 3:2 ratio.
Finally, let’s look at the problem from the video about markers in a box. We have a box that’s 4½ inches wide. How many ¾-inch markers will fit? If we’re uncertain about dividing fractions (we would calculate 4½ ÷ ¾) we could use a ratio table:
This student discovered that the ratio ¾ : 4½ is the same ratio as 1:6. So six markers will fit in the box.
How did they do it? To get 1 in the ¾ column, the student had to multiply 3/4 by 4/3. But remember the rule: in a ratio, if you multiply both numbers by the same factor, you have the same ratio. So in the table, the student multiplied the 3/4 by 4/3, and also multiplied the 4½ by 4/3. To do that, he or she converted to an “improper” fraction, 9/2, performed the multiplication, and reduced the result to simplest form (6).
That is, this student did all of the calculations using fraction multiplication (which is easy) and avoiding fraction division (which is hard).
If a student is thinking this way, you have a great “in” for helping them explain why “Invert and multiply” makes sense for dividing fractions. The reciprocal is what you have to multiply by in order to make a unit ratio.